If tan x = 3/2 tan 2(arctan(3/2)) = 12/5 = 24 arctan (3/2) = 5631° 2×5631° = ° tan ° = 12/5 = 24Tan(x y) = (tan x tan y) / (1 tan x tan y) sen(2x) = 2 sen x cos x cos(2x) = cos ^2 (x) sen ^2 (x) = 2 cos ^2 (x) 1 = 1 2 sen ^2 (x) tan(2x) = 2 tan(x) / (1Check https//mathstackexchangecom/q/ Yes, your answer is correct You can continue simplification First of all, you can conclude that (1\tan x)^2= (1\frac {\sin x} {\cos x})^2= (\frac {\sin x\cos x} {\cos x})^2=\frac {12\sin x \cos x} {\cos^2x} Yes, your answer is correct
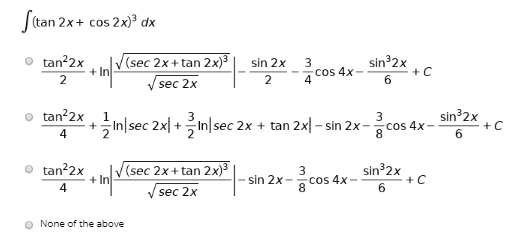
Answered Stan 2x Cos 2x Dx Tan 2x 2 V Sec 2x Bartleby
Tan 2x derivative
Tan 2x derivative-Integreren is een basisbewerking uit de analysengezien integreren niet, zoals bij differentiëren, door eenvoudige regels plaatsvindt, zijn tabellen met veel voorkomende integralen een handig hulpmiddelIn de onderstaande lijst van integralen wordt van een groot aantal verschillende functies de primitieve functie gegeven Er zijn lijsten van integralen2503 · The derivative of tan(2x) can be found by using the quotient rule and the chain rule Using the quotient rule, the tangent of 2x can be simplified to read the cosine squared of 2x plus the sine squared of 2x divided by the cosine squared of 2x Using the Pythagorean identity, this equation further simplifies to one over the cosine squared of 2x



What Is Integral Of Sin2x Tan2x Quora
· I have two problems I am stuck on, if you could show me how to solve the problems it would be much appreciated 1) Find sin 2x, cos 2x, and tan 2x from the given information tan x = − 1/6, cos x > 0 sin 2x = cos 2x = tan 2x = calculus Find complete length of curve r=a sin^3(theta/3) · Don't forget that you have the function as the exponent of the another function! · The equation $\tan x = \tan 2x \tan 4x \tan 8x$ Ask Question Asked today Active today Viewed 6 times 0 $\begingroup$ In the question we
Derive the expression 1 tan^2x Get the answer to this question and access a vast question bank that is tailored for studentsSolution) Given, Adjacent side (A)= 8 cm Opposite side (OTan(3x) in terms of tan(x), write tan(3x) in terms of tan(x), using the angle sum formula and the double angle formulas, simplifying trig identities, trigono
Tan(2x) = 2 tan(x) / (1 tan ^2 (x)) sin ^2 (x) = 1/2 1/2 cos(2x) cos ^2 (x) = 1/2 1/2 cos(2x) sin x sin y = 2 sin( (x y)/2 ) cos( (x y)/2 ) cos x cos y = 2 sin( (x y)/2 ) sin( (x y)/2 ) · 1tan^2x=sec^2x Change to sines and cosines then simplify 1tan^2x=1(sin^2x)/cos^2x =(cos^2xsin^2x)/cos^2x but cos^2xsin^2x=1 we · Example 14 Show that tan 3𝑥 tan 2𝑥 tan 𝑥 = tan 3𝑥 – tan 2𝑥 – tan 𝑥 We know that 3𝑥 = 2𝑥 𝑥 Therefe, tan 3𝑥 = tan(2𝑥 𝑥
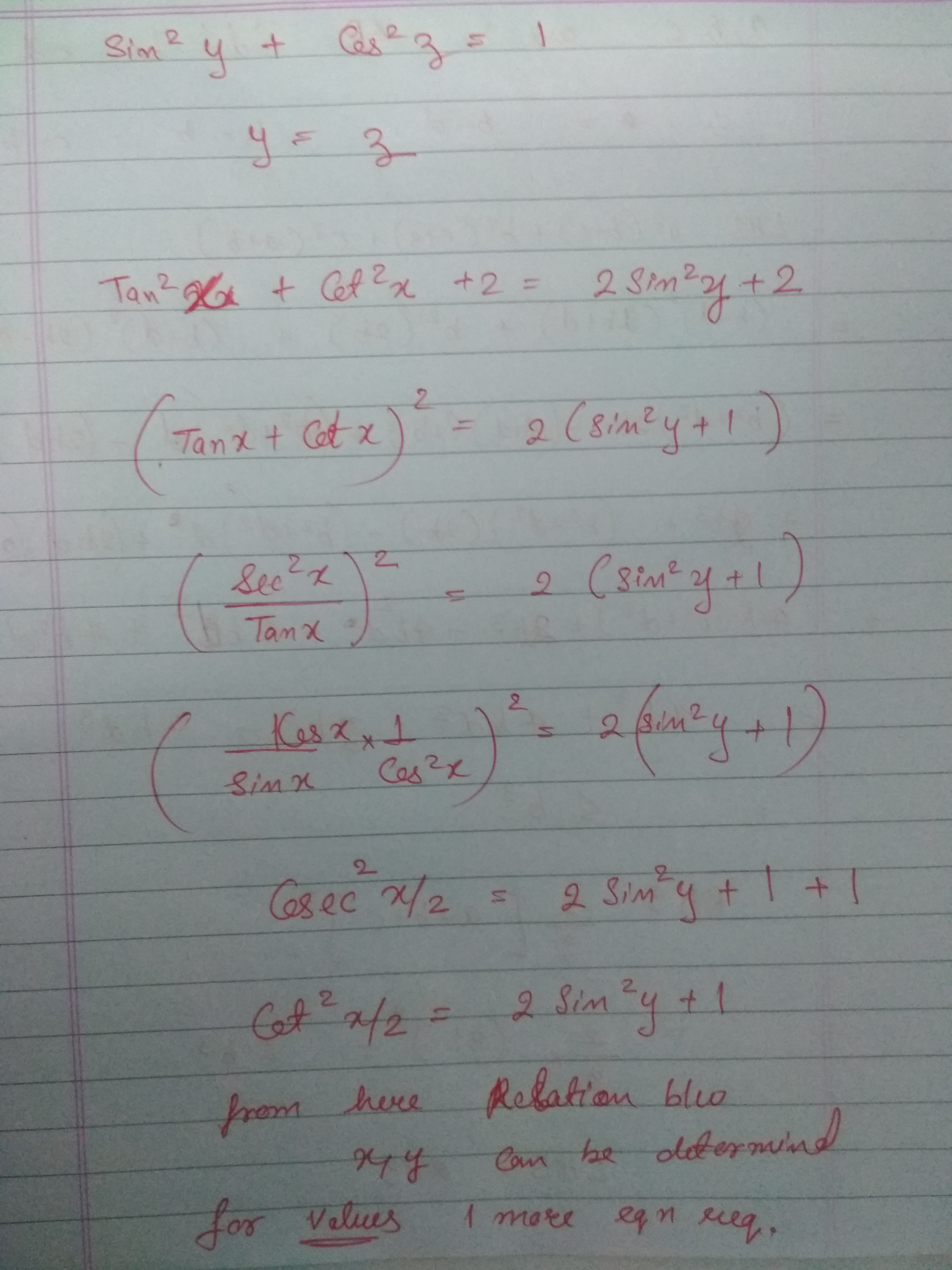


Solve For X Y And Z If Tan 2x Cot 2x 2sin 2y And Sin 2y Cos 2z 1 Askiitians



Prove Tan2x 2tanx 1 Tan 2 X Maths Introduction To Trigonometry Meritnation Com
· Use tan x=sinx/cos x, sin 2x = 2 sin x cos x and cos 2x = cos^2xsin^2x, for the right hand side expression 2 tan x/(1tan^2x)=(2sin x/cos x)/(1(sin^2x/cos^2x) =2 sin x cos x/(cos^2xsin^2x) =(sin 2x)/(cos 2x)=tan 2x Proofs for sin 2x = 2 sin x cos x and cos 2x = 1 2 sin^2x Use Area of a triangleABC = 1/2(base)(altitude) = 1/2 bc sin ASolve for x tan(2x)=1 Take the inverse tangent of both sides of the equation to extract from inside the tangent The exact value of is Divide each term by and simplify Tap for more steps Divide each term in by Cancel the common factor of Tap for more steps Cancel the common factor Divide by Multiply\(Tan 2x =\frac{2tan x}{1tan^{2}x} \) let's recall the addition formula \(tan(ab) =\frac{ tan a tan b }{1 tan a tanb}\) So, for this let a = b , it becomes \(tan(aa) =\frac{ tan a tan a }{1 tan a tana}\) \(Tan 2a =\frac{2tan a}{1tan^{2}a} \) Practice Example for tan 2 theta Question Find tan 2 x, if tan x



The General Solution Of The Equation Tanx Tan2x Tanx Tan2x 1 Is Youtube



Solve The Following Equation Tan X Tan 2x Tan 3x 0
Sin(x) = sqrt(1cos(x)^2) = tan(x)/sqrt(1tan(x)^2) = 1/sqrt(1cot(x)^2) cos(x) = sqrt(1 sin(x)^2) = 1/sqrt(1tan(x)^2) = cot(x)/sqrt(1cot(x)^2) tan(x) = sin(xIn various applications of trigonometry, it is useful to rewrite the trigonometric functions (such as sine and cosine) in terms of rational functions of a new variable These identities are known collectively as the tangent halfangle formulae because of the definition of These identities can be useful in calculus for converting rational functions in sine and cosine to functions of t in order · In this section we look at how to integrate a variety of products of trigonometric functions These integrals are called trigonometric integralsThey are an important part of the integration technique called trigonometric substitution, which is featured in Trigonometric SubstitutionThis technique allows us to convert algebraic expressions that we may not be able


If Tan X Cot X 2 Find The Value Of Tan 2x Cot 2x
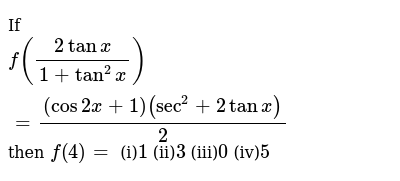


If F 2tanx 1 Tan 2 X Cos2x 1 Sec 2 2tanx 2 Then F 4
Like other substitutions in calculus, trigonometric substitutions provide a method for evaluating an integral by reducing it to a simpler one Trigonometric substitutions take advantage of patterns in the integrand that resemble common trigonometric relations and are most often useful for integrals of radical or rational functions that may not be simply evaluated by other methods0211 · So to find the second derivative of tan(2x), we just need to differentiate 2sec 2 (2x) We can use the chain rule to find the derivative of 2sec 2 (2x) (bearing in mind that the derivative of sec^2(x) is 2sec 2 (x)tan(x)) and it gives us a result of 8sec 2 (2x)tan(2x) The second derivative of tan(2x) is 8sec 2 (2x)tan(2x) · What Is The Integral of cos^2x this process is the reverse of finding a derivative Integrations are the antiderivatives Integrations are the way of


Evaluate Limx 0 X 2 Tan 2x Tan X Sarthaks Econnect Largest Online Education Community


Solved Consider The Possible Identity Tan 2x Cos 2x 1 Cos 2x Sec 2x A State Any Non Permissible Values B Attempt To Verify Possible Identity Course Hero
Graph y=tan(2x) Find the asymptotes Tap for more steps For any , vertical asymptotes occur at , where is an integer Use the basic period for , , to find the vertical asymptotes for Set the inside of the tangent function, , for equal to to find where the vertical asymptote occurs forFree trigonometric equation calculator solve trigonometric equations stepbystep · lim (x tan 2x 2x tan x)/(1 cos 2x)2 (for x → 0) is (a) 2 (b) 2 (c) 1/2 (d) 1/2 Welcome to Sarthaks eConnect A unique platform where students can interact with teachers/experts/students to get solutions to their queries



1 Tan 2x 1 Tan 2 X 1 2cos 2 X Youtube



Prove That Sin X Sin 3x Cos X Cos 3x Tan 2x Mathematics Shaalaa Com
Purplemath In mathematics, an "identity" is an equation which is always true These can be "trivially" true, like "x = x" or usefully true, such as the Pythagorean Theorem's "a 2 b 2 = c 2" for right trianglesThere are loads of trigonometric identities, but the following are the ones you're most likely to see and use∫ (cos 2x 1)/(cos 2x 1) dx = \(\int\frac{cos\,2x1}{cos2x1}\) dx = A tan x – x C B x tan x C C x – tan x C D –x – cot x CClick here👆to get an answer to your question ️ Differentiate the following from first principle tan 2x



Lim X Rightarrow Frac Pi 2 Frac Tan 2x Scholr



Answer The Following Questions Find The General Solution Of Tan 2x 0 Youtube
· Example 22 Find the derivative of tan (2x 3) Let y = tan (2x 3) We need to find derivative of y, ie 𝑑𝑦/𝑑𝑥 = (𝑑 tan〖(2𝑥3)〗)/𝑑𝑥715 K views 36 K people like thisSee the answer Show transcribed image text Expert Answer Previous question Next question Transcribed Image Text



Answered Find Sin 2x Cos 2x And Tan 2x From Bartleby



A Dfractanx1 Tan2x See How To Solve It At Qanda
Free derivative calculator differentiate functions with all the steps Type in any function derivative to get the solution, steps and graphTanx = t Sec^2 x dx= dt So now it is, 1/ (1t)^2 dt This integral is given by 1/1t and t= tanx So, it is cosx/cosx sinx tanx = t Sec^2 x dx= dt So now it is, 1/ (1t)^2 dt This integral is given by 1/1t and t= tanx So, it is cosx/cosx sinx Integral of the function \frac {\cos ^2 x} {1\tan x}Identities related to sin 2x, cos2x, tan 2x, sin3x, cos3x, and tan3x Sin 2x = Sin 2x = sin(2x)=2sin(x) cos(x) Sin(2x) = 2 * sin(x)cos(x) Proof To express Sine, the
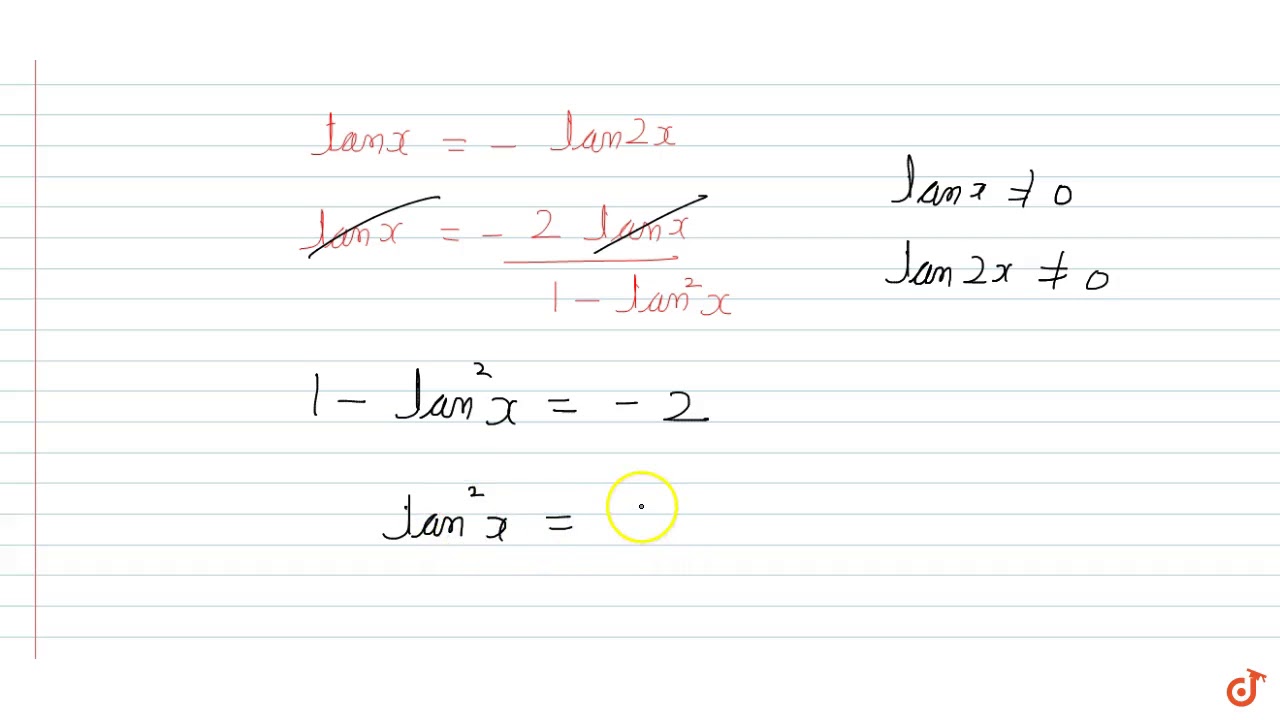


The General Solution Of The Equation Tanx Tan 2x Tan 2x Tanx 2 0 Is Youtube
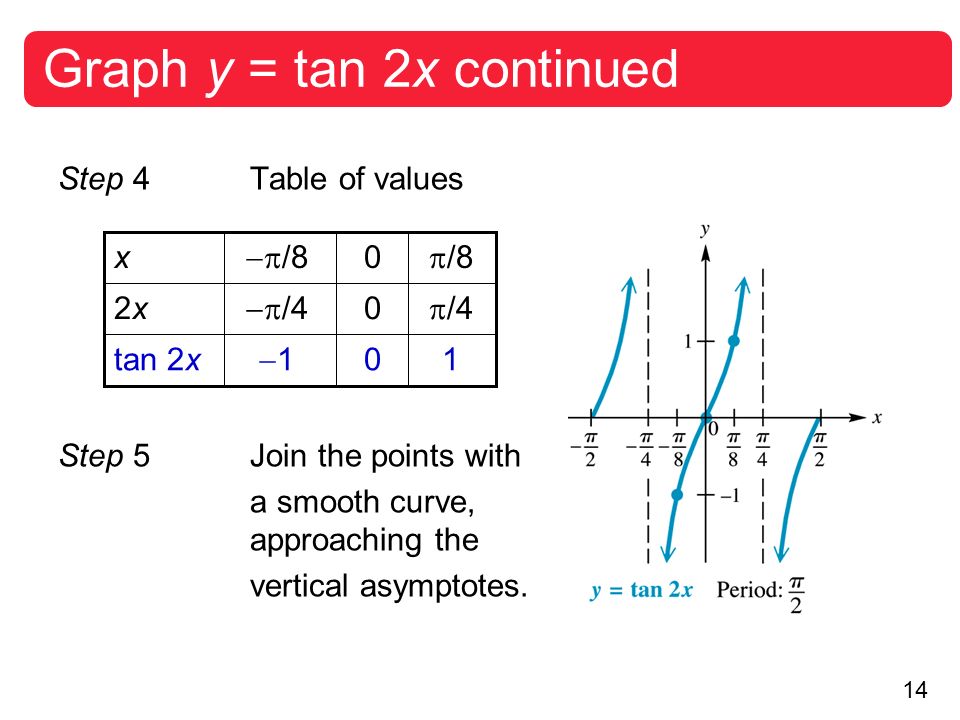


Howto How To Find Vertical Asymptotes Of Tan2x
In mathematics, the trigonometric functions (also called circular functions, angle functions or goniometric functions) are real functions which relate an angle of a rightangled triangle to ratios of two side lengths They are widely used in all sciences that are related to geometry, such as navigation, solid mechanics, celestial mechanics, geodesy, and many othersHere is the hint Let y = lim x→π/4 (tan (x))^ (tan (2x)) Then, perform logarithms, and we have ln (y) = lim x→π/4 tan (2x) * ln (tan (x)) Mod note Removed$$ \tan^2x \sec^2x $$ $$ (\sin x / \cos x)^2 (x / \cos x)^2 $$ trigonometry Share Cite Follow edited Jan 17 '13 at 644 Paul 176k 3 3 gold badges 48 48 silver badges 77 77 bronze badges asked Jan 17 '13 at 639 sam sam 61 1 1 gold badge 3 3 silver badges 6 6 bronze badges $\endgroup$ 1 4



Solution Solve For X In The Given Equation Arc Tan 2x Arctan X P



What Is Integral Of Sin2x Tan2x Quora
· I have two problems I am stuck on, if you could show me how to solve the problems it would be much appreciated 1) Find sin 2x, cos 2x, and tan 2x from the given information tan x = − 1/6, cos x > 0 sin 2x = cos 2x = tan 2x = calculus Find complete length of curve r=a sin^3(theta/3)2221 · Tan 2x can also be written in terms of sin x and cos x, Tan2x Formula in terms of cos x = \\frac{2 sin(x) cos(x)}{cos^{2}x sin^{2}x}\ Solved Examples Question 1) Calculate the tangent angle of a right triangle whose adjacent side and opposite sides are 8 cm and 6 cm respectively? · Solution for Find sin(2x), cos(2x), and tan(2x) from the given information sin(x) = 5 13, x in Quadrant I sin(2x) = cos(2x) = tan(2x) =



Double Angle Formulas Trigonometry Teachoo 2x 3x Formula Provi


What Is The Formula Of Tan2x Quora
Get answer Differentiate (tanx tan 2x tan 3x tan 4x) wrt x Getting Image Please Wait or Differentiate (tanx tan 2x tan 3x tan 4x) wrt x Apne doubts clear karein ab Whatsapp par bhi Try it now CLICK HERE 1x 15x 2x Loading DoubtNut Solution for you Watch 1000 concepts & tricky questions explained! · => `tan^2x` This proves that `tan^2 x = (1 cos(2x))/(1 cos(2x))` Approved by eNotes Editorial Team We'll help your grades soarCompute answers using Wolfram's breakthrough technology & knowledgebase, relied on by millions of students & professionals For math, science, nutrition, history



Chứng Minh Cac đẳng Thức Lượng Giac Tan 2x Sin 2x Tan 2x Sin 2x Toan Học Lớp 10 Bai Tập Toan Học Lớp 10 Giải Bai Tập Toan Học Lớp 10



Tema Angulo Doble Siendo Tan 45 X 1 3 Hallar El Valor De Tan 2x Brainly Lat
Find Sin(2x), Cos(2x), And Tan(2x) From The Given Information 8 Sin(x) = X In Quadrant III 17 = Sin(2x) = Cos(2x) = Tan(2x) = This problem has been solved!Show that tan 3x tan 2x tan x =tan 3xtan2xtanx Apne doubts clear karein ab Whatsapp par bhi Try it now CLICK HERE 1x 15x 2x Loading DoubtNut Solution for you Watch 1000 concepts & tricky questions explained!Tan(2x) is a doubleangle trigonometric identity which takes the form of the ratio of sin(2x) to cos(2x) sin(2 x) = 2 sin(x) cos(x) cos(2 x) = (cos(x))^2 – (sin(x))^2 =
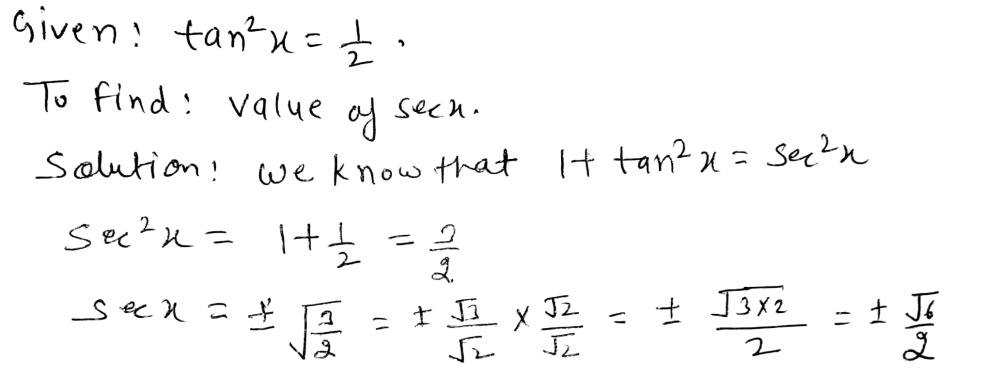


Byjok H9 9y3gm



Diketahui Sin X A Nilai Tan 2x Adalah Brainly Co Id
WolframAlpha brings expertlevel knowledge and capabilities to the broadest possible range of people—spanning all professions and education levels



Differentiate The Following From First Principle Tan 2x



Show That Tan3xtan2xtanx Tan3x Tan2x Tanx Mathematics Topperlearning Com Dc9390xx



3 Simplifying Trig Expression 1 Tan 2x Youtube



Tan 2x Formula Learn Formula For Calculating The Double Angle Tan 2x



Ex 3 4 8 Find General Solution Of Sec 2 2x 1 Tan 2x Teachoo



Differentiate The Following From First Principle Tan 2x 1



Ex 3 4 8 Find General Solution Of Sec 2 2x 1 Tan 2x Teachoo



Cbse Class 11 Sin 2x Sin 3x Cos 2x Cos 3x Tan 2x Tan 3x Offered By Unacademy



Sec22x 1 Tan 2x Find The General Solution Maths Trigonometric Functions Meritnation Com
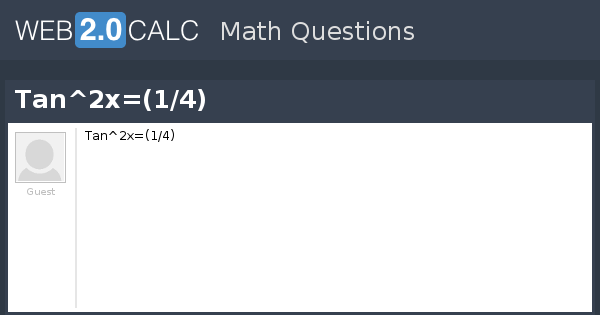


View Question Tan 2x 1 4



Tan 2x Identity Learn Lif Co Id



Tan2x Formula In Terms Of Tan Edurev Class 12 Question
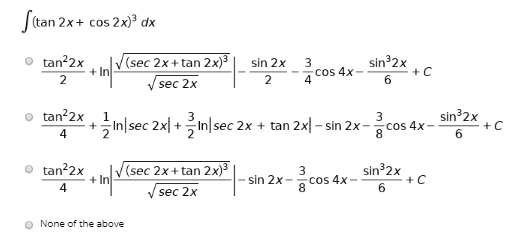


Answered Stan 2x Cos 2x Dx Tan 2x 2 V Sec 2x Bartleby



How To Integrate Tan 2x Youtube Cute766



Tan Graphs Circular Functions


A Trig Identity



Tangent For Sum Of Double Angle Shortmath
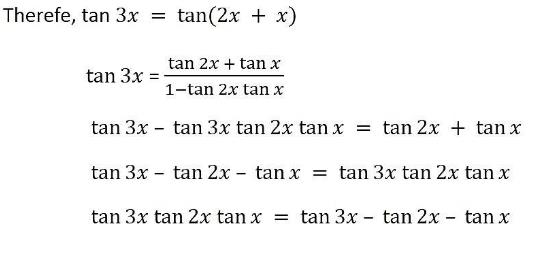


Prove That The Differentiation Of Tan3x Tan2x Tanx Is 3sec 3x 2sec 2x Sec X Edurev Class 12 Question



Find Sin 2x Cos 2x And Tan 2x From The Given Information Image Select The Correct Answer Ppt Download


What Is The Formula Of Tan2x Quora



Tan 7x Tan 2x 2 Tan 5x Brainly In



How Do You Simplify Sec 4x Tan 4x Sec 2x Tan 2x Socratic



Solved Verify The Identity 4 2 Tan X Secx2tan X 1 Whic Chegg Com



How Does One Verify Cos 2x Sin 2x 1 Tan 2x Cos 2x Socratic



How Do You Simplify 1 Tan 2 X 1 Tan 2 X Socratic



Solved Verify That The Equation Is An Identity Tan 2x Chegg Com


Limes Tan 2x X Berechnen Mathelounge



Show That The Following Are Not Trigonometric Identities 1 Tan 2x 2tan X 2 Sec X Sqrt 1 Tan 2 X 3 Sin X Y Sin X Sin Y Study Com



Prove That Tan 8x Tan 6x Tan 2x Tan 8x Tan 6x Tan 2x Maths Meritnation Com


Find The Period Of Tan 2x Class 10 Maths Cbse



Find The General Solution For Each Of The Following Equations Sec2 2x 1 Tan 2x Mathematics Shaalaa Com
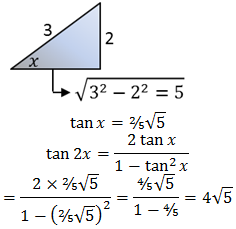


Tangent For Sum Of Double Angle Shortmath



Example 22 Find Derivative Of Tan 2x 3 Chapter 5 Class 12



Tan 2xの不定積分で Sin 2から1 Cos 2xになるのはなぜでしょうか Clear



Integral Of Tan 2x Cot 2x 2 Calculus 1 Trig Integrals Calculus Mathematics Email Subject Lines


What Is The Formula Of Tan2x Quora



Tan2x 2tanx 1 Tan X Trigonometric Identity Solve Hindi Youtube



F X Tan 2x X 1767 Is 506 2 Continous Ab Y La Then 19 A Is Ca 1 2 62 62 4 D 1 2



Find The Derivative Of The Function Y Sin Tan 2x Homework Help And Answers Slader
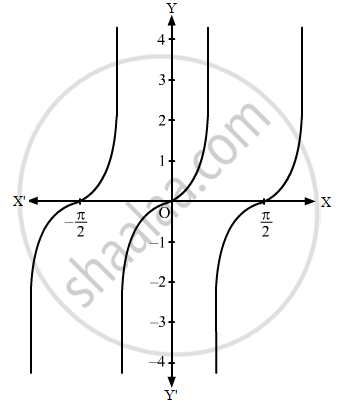


Sketch The Graphs Of The Following Functions F X Tan 2x Mathematics Shaalaa Com


How To Prove Csc 2x 1 Tan 2x 1 Is Equivalent To Cosec 2x Quora



Tan2x Acilimi Pow Bylge


Tan2x ただの悪魔の画像
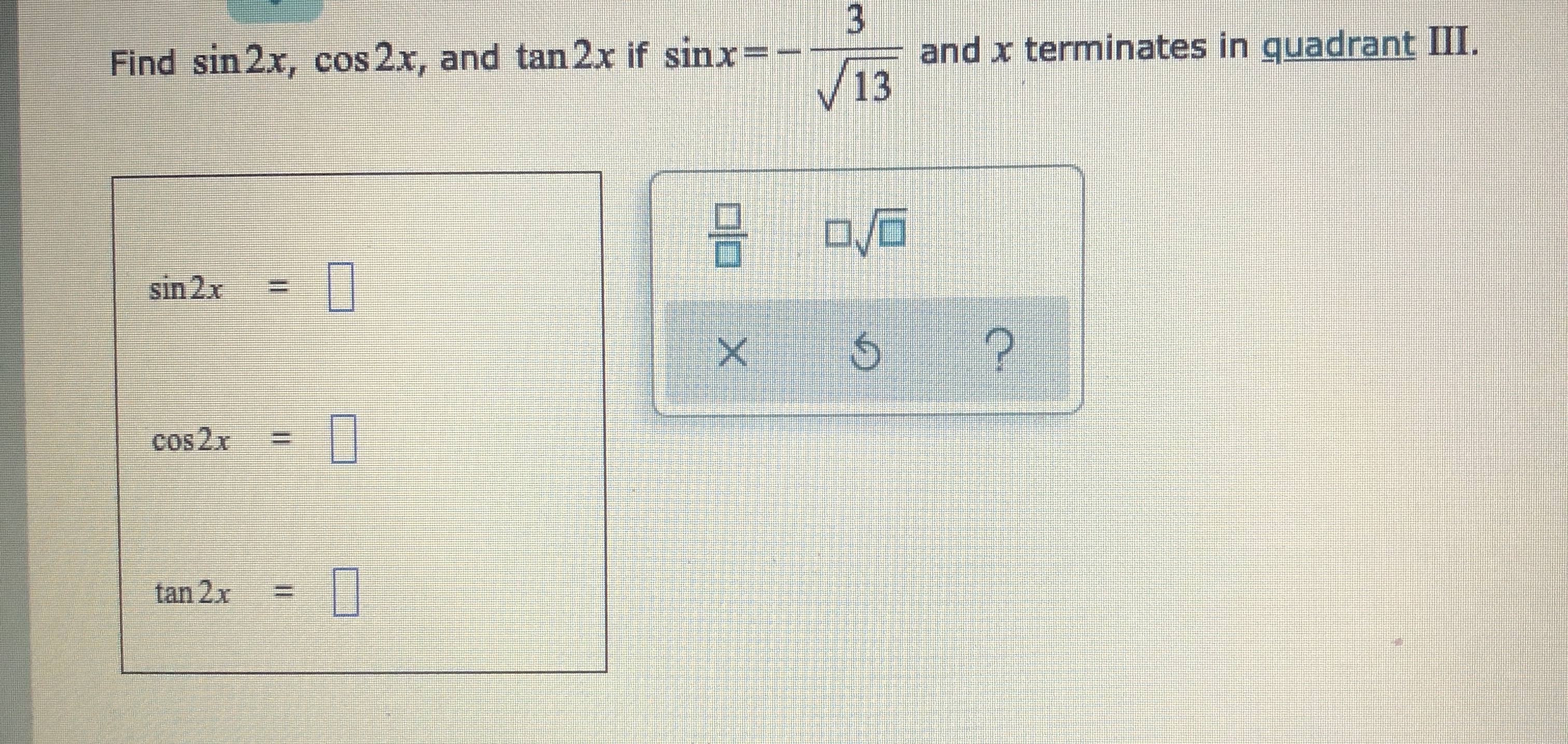


Answered Find Sin 2x Cos 2x And Tan 2x If Bartleby


Solution Determine The Period Of Y Tan 2x



How To Graph Tan Ex Y Tan2x Study Com



Integrate Sec 2x Method 1



Solve Tan 2x Tanx 0
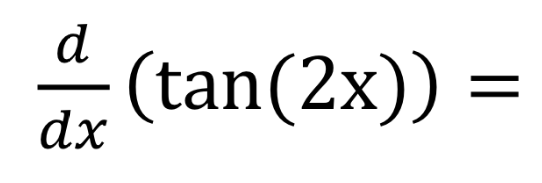


Solved D Dx Tan 2x Chegg Com



Ex 3 4 8 Find General Solution Of Sec 2 2x 1 Tan 2x Teachoo



The Derivative Of Tan 2x Derivativeit



Solved 1 Cot2x Tan2x Sec2x To See A Detailed Descrip Chegg Com



Solved Sketch The Graph Of The Following Functions Y Tan 2x Y Self Study 365



Solve The Question Tan X Tan 2 X Tan X Tan 2x 1 Brainly In



In This Solution Why The 2 Tan2x 1 Tan 2x Was Dived By1 2tan 2x 1 Tan 2x 2 Trigonometric Functions Q23 Prove That Solution 4tanx La Tan X Maths Trigonometric Functions Meritnation Com



How Do You Solve 1 Tan 2x 6 2sec 2x Socratic



If Tanx Tan 2x 1 Then The Value Of Tan 4x 2 Tan 3x Tan 2x



Tan2x Tan 2x Identity For Tan2x Proof Of Tan2x Identity Formula For Tan2x Youtube



Answered Find Sin 2x Cos 2x And Tan 2x From Bartleby



Find The Derivative Of The Given Function Y Tan 2x 1 Cot 2x I Tried Converting The Original Function In Terms Of Sin And Cos But It Was Still Too Complicated To Be Called Simplified
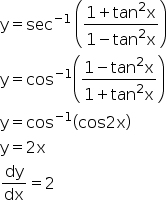


Differentiate Wrt X Sec 1 1 Tan2x 1 Tan2x Mathematics Topperlearning Com Nti7rxx
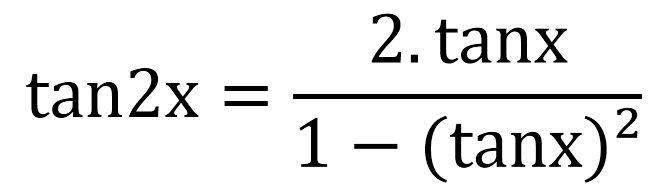


Tan2x Acilimi Pow Bylge



The General Solution Of Tanx Tan2x Tan3x Tanx Tan2x Tan3x
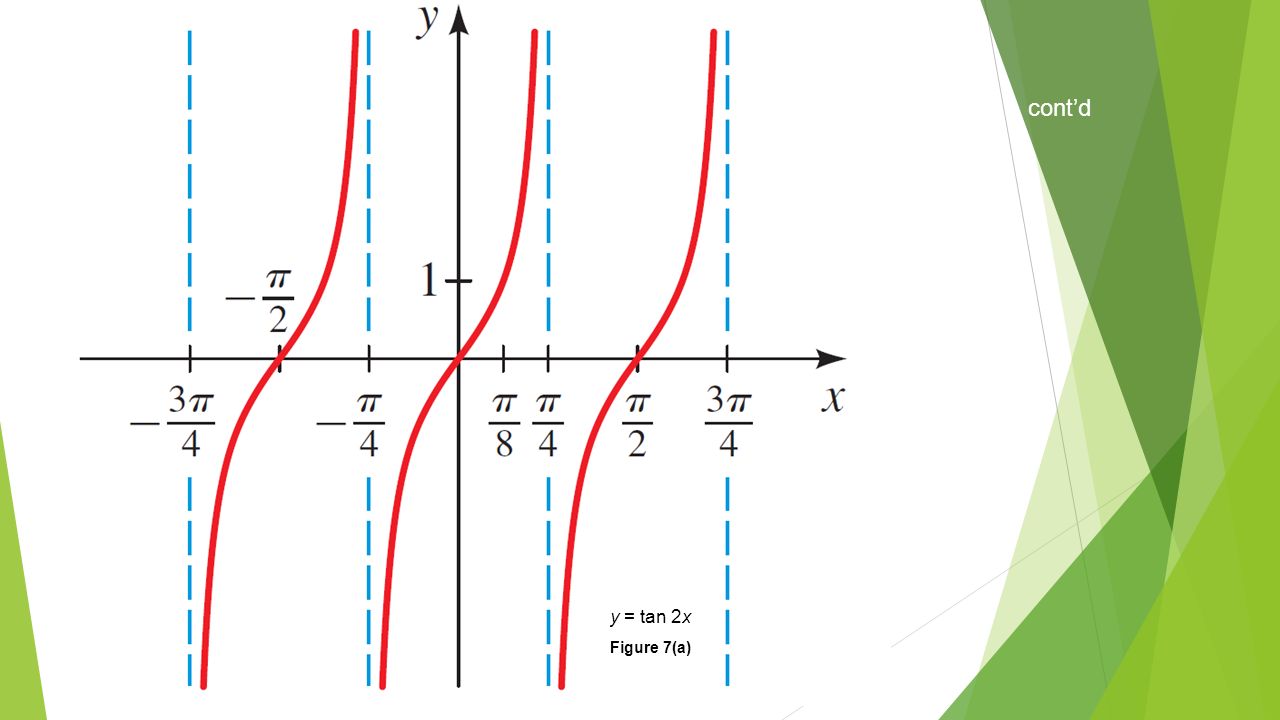


Graphs Of Tangent Cotangent Ppt Video Online Download



Integrate Tan 2x By Parts


Solution Show Me The Graph Of Y Tan2x Step By Step And How To Solve Keypoints


Show That Tan 3x Tan 2x Tan X Tan3x Tan 2x Tan X Sarthaks Econnect Largest Online Education Community



Qprove That Tan X 2 Tan 2x 4 Tan 4x 8 Cot 8x Cot X Mathematics Topperlearning Com Blpusg55



Cbse Class 11 Sin 2x Sin 3x Cos 2x Cos 3x Tan 2x Tan 3x Offered By Unacademy



Nhung Cong Thuc Luong Giac Co Ban



Lim X 0 Log Tan 2x Tan 2 2x


Find D X Sin Tan 2x Using Chain Rule Gauthmath


8 Solve The Equation Sec C22x See How To Solve It At Qanda


Graph Tangent And Cotangent


C2 Solve Tan2x 0 In The Interval 0 180 The Student Room


Integral Of Tan2x Cute766



0 件のコメント:
コメントを投稿